Unlocking The Mystery: What Is The Square Root Of 16?
Mathematics, at its core, is about understanding patterns and relationships. One of the most fundamental operations we encounter is the concept of a square root. While it might sound intimidating, it's actually quite intuitive and plays a crucial role in various fields, from geometry to engineering. Today, we're going to demystify this concept, specifically focusing on a very common and straightforward example: the square root of 16. By the end of this article, you'll not only understand what the square root of 16 is but also grasp the broader principles behind square roots, including how they apply to negative numbers and fractions.
What Exactly is a Square Root?
Before we dive into the specifics of 16, let's establish a clear understanding of what a square root is. In simple terms, the square root of a number is a value that, when multiplied by itself (or "squared"), gives you the original number. Think of it like reversing the squaring process. If you have a number, say 'x', and you multiply it by itself to get 'y' (so, x * x = y), then 'x' is the square root of 'y'. The symbol used to denote a square root is the radical symbol, written as √.
For instance, if we consider the number 9, we know that 3 multiplied by 3 equals 9 (3 * 3 = 9). Therefore, 3 is the square root of 9. Similarly, for 25, since 5 * 5 = 25, 5 is the square root of 25. It's a fundamental concept that helps us work backward from a squared number to its original base.
Finding the Square Root of 16: The Core Concept
Now, let's apply this understanding directly to our main subject: the number 16. Our goal is to find a number that, when multiplied by itself, results in 16. This is the very definition of the problem we are trying to solve.
Understanding the Problem
To find the square root of 16, we're asked to determine what number, when multiplied by itself (squared), equals 16. It's a straightforward question that requires us to recall our multiplication tables or think about numbers that are perfect squares.
The Solution: It's 4!
If you think about it, what number times itself gives you 16? Let's try a few:
- 1 × 1 = 1 (Too small)
- 2 × 2 = 4 (Still too small)
- 3 × 3 = 9 (Getting closer)
- 4 × 4 = 16 (Exactly what we're looking for!)
Principal vs. Negative Square Roots
While 4 is indeed the number we're looking for, it's important to understand a nuance in square roots. Every positive number actually has two square roots: a positive one and a negative one. This is because when you multiply a negative number by a negative number, the result is a positive number.
Consider -4:
- -4 × -4 = 16
Beyond Positive Numbers: The Square Root of -16
What happens when we try to find the square root of a negative number, like -16? This introduces us to a fascinating concept in mathematics: imaginary numbers. You might instinctively try to find a number that, when multiplied by itself, gives you -16. However, as we saw:
- A positive number multiplied by a positive number yields a positive result (e.g., 4 × 4 = 16).
- A negative number multiplied by a negative number also yields a positive result (e.g., -4 × -4 = 16).
This means there is no "real" number that, when squared, will give you a negative result. To find the square root of -16, we need to consider the concept of imaginary numbers, as the square root of a negative number involves these.
Mathematicians introduced the imaginary unit, denoted by 'i', where 'i' is defined as the square root of -1 (i.e., i = √-1). Using this, we can find the square root of -16:
- We can express negative sixteen as the product of 16 and -1:
√-16 = √(16 × -1) - Apply the property of square roots that allows us to separate the product:
√(16 × -1) = √16 × √-1 - We already know that the square root of 16 is 4, and by definition, the square root of -1 is 'i':
√16 × √-1 = 4 × i - Therefore, the square root of -16 is 4i.
This demonstrates how the concept of square roots extends beyond just real numbers into the realm of complex numbers, which are essential in advanced mathematics, physics, and engineering.
Square Roots in Action: Other Examples and Applications
Understanding the square root of 16 is a great starting point, but square roots appear in many different forms and calculations. Let's look at a few more examples to solidify our understanding and see how these principles apply.
Sums Inside Square Roots
Sometimes, you'll encounter expressions where you need to perform an operation before finding the square root. For example, to compute the square root of the expression 16 + 64 + 64, you follow these steps:
- Calculate the sum inside the square root: First, add the numbers inside the square root:
16 + 64 + 64 = 144 - Then, find the square root of the sum:
√144 = 12
This shows that you must complete the operation within the radical first before extracting the root.
Simplifying Products with Square Roots
Another common scenario is simplifying square roots of numbers that aren't perfect squares. Consider an expression like √48. While 48 isn't a perfect square, we can simplify it by finding perfect square factors within it. We want to find a perfect square that divides 48. We know that 16 is a perfect square (4 × 4 = 16) and 16 divides 48 (48 ÷ 16 = 3).
Therefore, we can rewrite √48 as:
- √48 = √(16 × 3)
- Separate the square roots: √16 × √3
- Calculate the square root of the perfect square: 4 × √3
- So, √48 simplifies to 4√3.
This technique is crucial for simplifying expressions and is often encountered when dealing with the Pythagorean theorem or other geometric calculations.
Square Roots of Fractions
Square roots can also apply to fractions. The principle is simple: you find the square root of the numerator and the square root of the denominator separately. For instance, let's consider the square root of 121/16.
- √(121/16) = √121 / √16
- We know √121 = 11 (since 11 × 11 = 121) and √16 = 4.
- So, the square root of 121/16 is indeed 11/4.
Similarly, if we need to find the square root of 16/81:
- √(16/81) = √16 / √81
- We know √16 = 4 and √81 = 9 (since 9 × 9 = 81).
- Therefore, the principal square root of 16/81 is 4/9. And just like with whole numbers, the negative square root is -4/9.
In fraction form, this means that if you take a square with an area of 16 square units and divide it into 81 equal parts, the side length of the original square would be 4 units, and the side length of a square with area 81 would be 9 units. This concept is fundamental in understanding ratios and scaling in geometry.
Practical Applications
Square roots are not just abstract mathematical concepts; they have numerous real-world applications. They are essential in:
- Geometry: Calculating the sides of right-angled triangles using the Pythagorean theorem (a² + b² = c²), finding the side length of a square given its area, or determining distances in coordinate geometry.
- Physics: Formulas involving speed, acceleration, and energy often incorporate square roots.
- Engineering: Used in designing structures, circuits, and understanding material properties.
- Statistics: Calculating standard deviation, which measures the dispersion of a set of data.
Conclusion
In this lesson, we explored the concept of square roots and focused on finding the square root of 16. We learned that the square root of a number is the value that, when multiplied by itself, gives the original number. For 16, that number is 4. We also delved into the distinction between the principal (positive) square root and its negative counterpart, understanding that both 4 and -4 are square roots of 16, but 4 is the principal one.
Furthermore, we ventured into the intriguing world of imaginary numbers to comprehend the square root of negative numbers like -16, discovering that it involves the imaginary unit 'i'. We also saw how square root principles apply to more complex scenarios, such as sums inside square roots, simplifying non-perfect squares, and finding the square roots of fractions. The ability to work with square roots is a foundational skill that opens doors to understanding more complex mathematical concepts and their applications across various scientific and technical disciplines.
Summary: This article thoroughly explains the concept of square roots, specifically focusing on the square root of 16. It defines what a square root is, identifies 4 as the principal square root of 16, and clarifies the difference between principal and negative square roots. The discussion extends to the square root of negative numbers, introducing imaginary numbers with √-16 as an example. Additionally, the article illustrates the application of square root principles through various examples, including sums inside square roots (e.g., √144), simplifying non-perfect squares (e.g., √48), and finding square roots of fractions (e.g., √121/16, √16/81). It concludes by emphasizing the practical importance of square roots in everyday mathematics and real-world applications.

Square Root of 16 - How to Find the Square Root of 16? - Cuemath
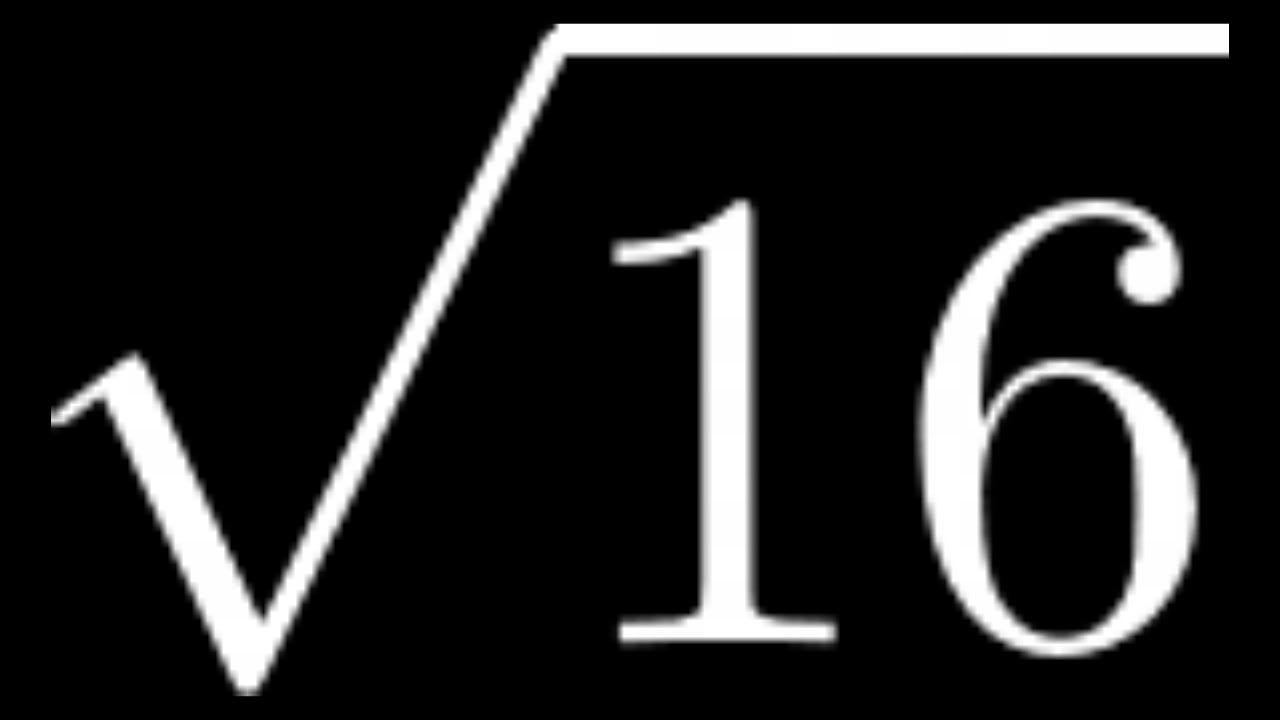
How to Simplify the Square Root of 16: sqrt(16) - YouTube

Square root of -16 || Square root of a negative number || Root(-16