Master The Rectangle: Your Ultimate Guide To Finding The Perimeter
Have you ever wondered how much fencing you'd need for a garden, or how much trim to buy for a new picture frame? These everyday questions often boil down to a simple mathematical concept: perimeter. In geometry, the perimeter is the total distance around the outside of a two-dimensional shape. For common shapes like rectangles, calculating the perimeter is a straightforward process that's incredibly useful in many real-world scenarios. This article will walk you through everything you need to know about finding the perimeter of a rectangle, from the basic formula to more advanced scenarios.
Understanding the Basics: What is Perimeter?
Before diving into rectangles specifically, let's solidify our understanding of perimeter in general. Imagine walking along the edge of any shape; the total distance you cover is its perimeter. In simpler terms, the perimeter of a shape is the sum of the lengths of all its sides. This fundamental definition holds true for all polygons, including our focus shape: the rectangle.
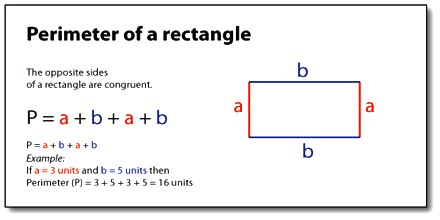
A rectangle is a four-sided shape where opposite sides are equal in length and all four angles are right angles (90 degrees). This unique property simplifies the perimeter calculation significantly. Instead of adding four potentially different side lengths, we only need to concern ourselves with two distinct measurements: its length and its width. The perimeter of a rectangle is the sum of all its sides' lengths. Since a rectangle has two lengths and two widths, we can simplify this sum.
The Fundamental Formula for a Rectangle's Perimeter
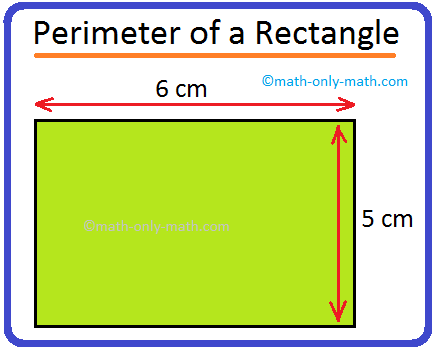
Thanks to the consistent properties of a rectangle, there's a very simple and efficient formula to calculate its perimeter. To find the perimeter of a rectangle, use the formula P = 2 × (length + width). This formula is incredibly versatile and is the go-to method for most perimeter calculations involving rectangles. It can also be expressed as P = 2l + 2w, where 'P' represents the perimeter, 'l' represents the length, and 'w' represents the width of the rectangle.
Let's break down why this formula works. As established, a rectangle has two sides of equal length and two sides of equal width. So, if you were to add up all four sides individually, you'd be doing: length + width + length + width. By grouping these terms, you get (length + length) + (width + width), which simplifies to 2 × length + 2 × width. Factoring out the '2' gives us 2 × (length + width). It's a neat shortcut that saves time and effort.
Step-by-Step Calculation Using the Formula
Using the formula P = 2 × (length + width) is incredibly straightforward. Here's how to apply it:
- Identify the Length (l) and Width (w): These are the two distinct dimensions of your rectangle. It doesn't matter which side you label as 'length' and which as 'width,' as long as you're consistent.
- Add the Length and Width: Perform the addition operation inside the parentheses first. For example, if your rectangle has a length of 9 meters and a width of 11 meters, you would first calculate (9 m + 11 m) = 20 m.
- Multiply the Sum by Two: Once you have the sum of the length and width, simply multiply that result by 2. This accounts for all four sides of the rectangle. Continuing our example, 2 * 20 m = 40 m.
So, for a rectangle with lengths 9 m and 11 m, the perimeter is 2*(9 m + 11 m), which equals 40 m. Let's look at another example provided in our data: The perimeter of rectangle PQRS is 113.4 meters, calculated using the formula P = 2 × (l + w). Given the length of 39.2 meters and width of 17.5 meters, the total perimeter is indeed 2 × (39.2 + 17.5) = 2 × 56.7 = 113.4 meters. As you can see, simply add the length and width, then multiply by 2. It's a consistent and reliable method.
Finding Perimeter When Sides Aren't Directly Given
Sometimes, you might not be handed the length and width on a silver platter. Instead, you might have other pieces of information, such as the coordinates of the rectangle's vertices or its area. Don't worry; with a few extra steps, you can still find the perimeter.
Using Coordinates to Determine Side Lengths
In a coordinate plane, shapes are defined by the points (vertices) that make them up. To find the perimeter of a rectangle in a coordinate plane, you first need to identify the coordinates of its vertices. Once you have these coordinates, you can determine the lengths of its sides.
For rectangles whose sides are parallel to the x and y axes, finding the length and width is quite simple: you just subtract the x-coordinates to find the horizontal length and subtract the y-coordinates to find the vertical width. For instance, to better understand how to find the perimeter and area, consider a different rectangle with vertices (1,2), (1,5), (4,2), and (4,5). The length would be the difference in the x-coordinates (4 - 1 = 3 units), and the width would be the difference in the y-coordinates (5 - 2 = 3 units). In this specific case, it's a square, but the principle applies to any rectangle. Once you have the length (3 units) and width (3 units), you can apply the perimeter formula: P = 2 × (3 + 3) = 2 × 6 = 12 units.
For rectangles that are rotated or not aligned with the axes, you would need to use the distance formula to find the length of each side. The distance formula, d = sqrt((x2 - x1)^2 + (y2 - y1)^2), calculates the distance between two points (x1, y1) and (x2, y2). To find the perimeter of rectangle ABCD, we can add up the lengths of all four sides. The lengths of the sides can be found by using the distance formula. For instance, if you know the coordinates of a rectangle's corners, you can apply the same method to find the lengths of the sides and then compute the perimeter and area. The perimeter of the rectangle is the sum of the length of its four sides. Once you've calculated the length of two adjacent sides (one length and one width), you can then proceed with the standard perimeter formula P = 2l + 2w.
When Area is Provided (Indirect Calculation)
Sometimes, you might be given the area of a rectangle and perhaps one of its side lengths, or a relationship between its length and width. The area of the rectangle provides us with another equation: Area = length × width (A = l × w). For example, if the area is 108 square units, then ab = 108 (where 'a' is length and 'b' is width). If you're also given that, say, the length is twice the width (a = 2b), you can substitute this into the area equation: (2b) × b = 108, which simplifies to 2b^2 = 108. Solving for 'b' would give you the width, and then you can find the length. With these two equations, we can solve for a and b to acquire the lengths of sides a and b. Having these dimensions, you can then easily calculate the perimeter using the formula P = 2l + 2w.
Real-World Applications of Perimeter
Understanding how to find the perimeter of a rectangle isn't just a classroom exercise; it has practical applications in countless real-world scenarios. Here are just a few examples:
- Home Improvement: If you're planning to put up a fence around your rectangular backyard, you'll need to know the perimeter to determine how much fencing material to buy. Similarly, if you're installing decorative trim or baseboards in a rectangular room, the perimeter tells you the total length of material needed.
- Gardening and Landscaping: When designing a rectangular garden bed, calculating the perimeter helps you figure out how much edging material or weed barrier fabric you'll need.
- Construction: Builders and architects frequently use perimeter calculations to estimate materials for foundations, framing, and other structural elements of rectangular buildings.
- Crafts and Hobbies: From sewing projects that require measuring fabric edges to framing artwork, perimeter calculations are essential for accurate material estimation.
- Sports: The boundaries of many sports fields (like soccer or football fields) are rectangular, and their perimeters are important for setting up games and understanding distances.
Conclusion
The perimeter of a rectangle is a fundamental concept in geometry with wide-ranging practical applications. Whether you're a student learning about shapes, a homeowner planning a DIY project, or a professional in a field that requires precise measurements, mastering the calculation of a rectangle's perimeter is an invaluable skill. By simply remembering the formula P = 2 × (length + width), you can easily determine the total distance around any rectangular object. Even when direct side lengths aren't given, methods like using coordinate points or leveraging area information allow you to find the necessary dimensions and then apply the core formula. So, the next time you encounter a rectangular shape, you'll have all the tools to confidently find its perimeter!
How to Calculate the Perimeter of a Rectangle? - Assignment Point

How Do You Find the Perimeter of a Rectangle? Instructional Video for
Perimeter of a Rectangle | How to Find the Perimeter of a Rectangle?